Fast and Robust Trajectory Optimization

Standard trajectory optimization methods based on direct multiple shooting or direct collocation generate open-loop state and control histories. To account for disturbances or unmodeled dynamics it is generally necessary to track these planned motions with a feedback controller. This decoupled approach to planning and control can fail when the planned trajectory provides insufficient margin for error in the controller’s tracking performance. For example, a trajectory which involves tightly maneuvering around obstacles may result in a collision when faced with disturbances arising from the environment (e.g. wind gusts) or the use of simplified dynamics (e.g. negleting tire physics on a car).

Robust trajectory optimization methods provide means for accounting for expected disturbances or unmodeled dynamics explicitly in the planning phase. One such method is DIRTREL, which embeds a time-varying linear quadratic regulator as a feedback law within a standard trajectory optimization method and then propagates uncertainty in a manner analogous to an extended Kalman filter. This yields ellipsoidal bounds which approximate the expected uncertainty in the states and controls. By applying the matrix square root operation, the principle axes of these ellipsoids can be extracted. The resulting points (analogous to sigma points in the EKF) can be incorporated within the objective and constraints of the trajectory optimization to achieve robustness.

One caveat of this sampling-based approach is that points within the ellipsoid not corresponding to sigma points may still violate constraints. Further, extrating these points requires embedding the matrix square root operation within a trajectory optimization problem. This is generally done using iterative algorithms such as Denman-Beavers, which is not guaranteed to converge. Lastly, as trajectory optimization is performed on discrete time representations of a continuous-time optimal control problem, constraint satisfication between discrete time indices is ignored. This is generally overcome by increasing the density of the time discretization at the cost of computational complexity.

In this work we propose a method that imposes constraints directly on the whole ellipsoid set rather than the sampled sigma points. Further we optionally allow the constraints to be imposed on the convex hull of an ellipsoid at two neighboring time indices. This yields connected funnels which are effective at preventing the solver from exploiting the discrete-time approximation of reality. As a result, we can safely use a large time step in our transcription method, yielding a smaller nonlinear program for computational efficiency. Our method builds upon our recent work in establishing differentiable signed distance representations for continuous collision avoidance.

As an initial demonstration, we consider a Dubin’s car model navigating two obstacles. Bounded additive and multiplicative uncertainty is introduced to the state equations. We solve the resulting trajectory optimization method using both DIRTREL and our proposed method with a time horizon of 3s and time step of 0.2s (N = 15). We then execute 100 simulations while varying the uncertainty within the stated bounds. In 12 instances DIRTREL fails to avoid the obstacle. This can been seen in the lower right subplot in which gray traces penetrate the obstacle in purple.

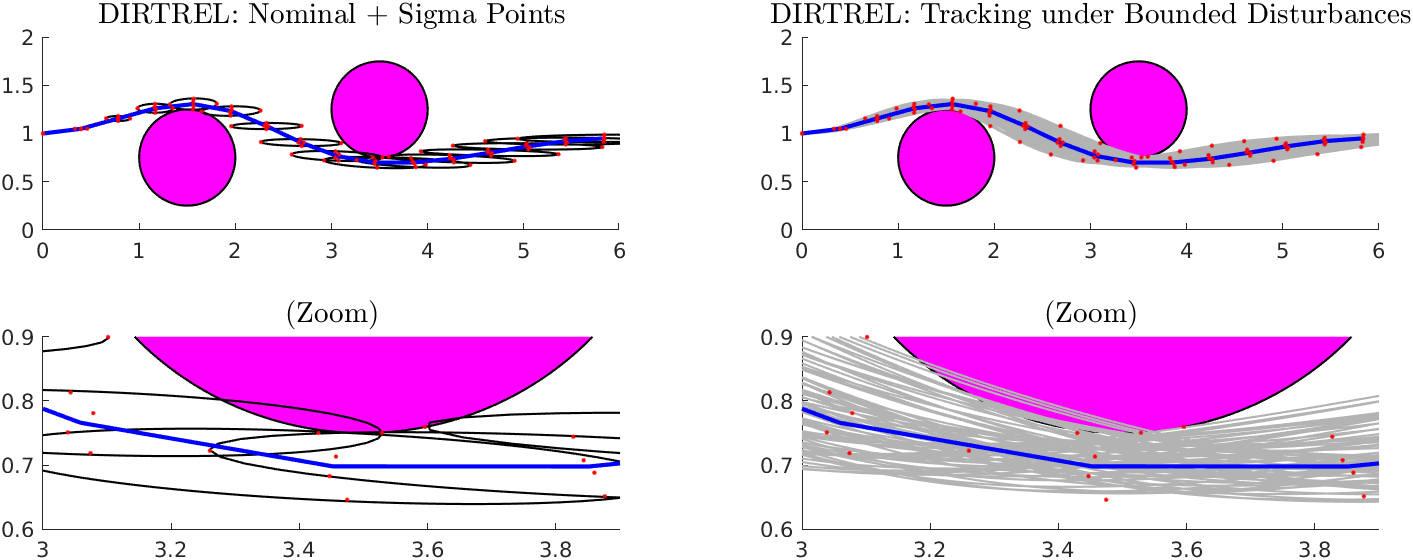
With our proposed method, no failures are experienced as shown below.

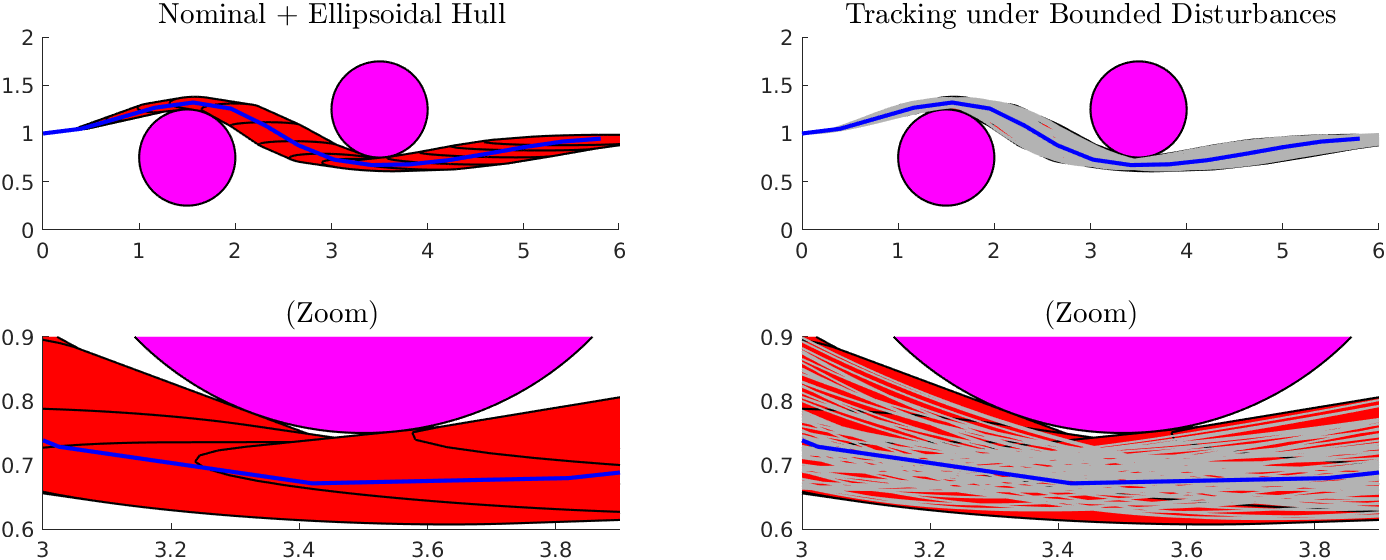
Further, by eliminating the Denman-Beaver’s operation, our resulting nonlinear program empirically has better convergence. With a simple initial guess, the DIRTREL solution took 5.31s while our proposed method took 0.73s. By leveraging speed options within the auto-diff tool (‘expand’ in CasADi) we were able to further reduce our runtime to 130ms. Thus our method shows promise for real-time robust trajectory optimization.