A Differentiable Signed Distance Representation for Continuous Collision Avoidance in Optimization-Based Motion Planning

Existing collision avoidance conditions in optimization-based motion planning only consider discrete time indices. This can lead to erroneous trajectories in which a vehicle passes through thin walls or cuts corners. Generally this is resolved by artificially inflating obstacles and/or using a finer time discretization. This comes at the expense of 1) reducing the possible configuration space, making tight maneuvering impossible or 2) increasing the computational complexity making real-time execution problematic.

In this work, we propose a new set of conditions for exactly representing collision avoidance constraints within optimization-based motion planning algorithms. The conditions are continuously differentiable and therefore suitable for use within standard nonlinear optimization solvers which require smooth expressions. We show how our formulation can be used to ensure continuous collision avoidance such that the vehicle does not cut corners or pass through obstacles.

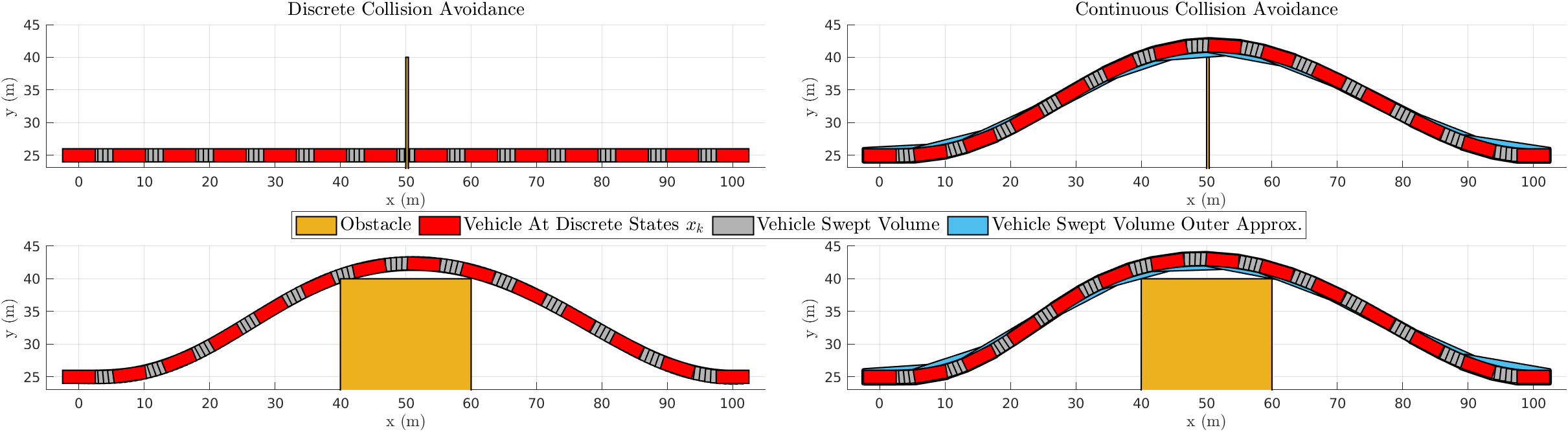
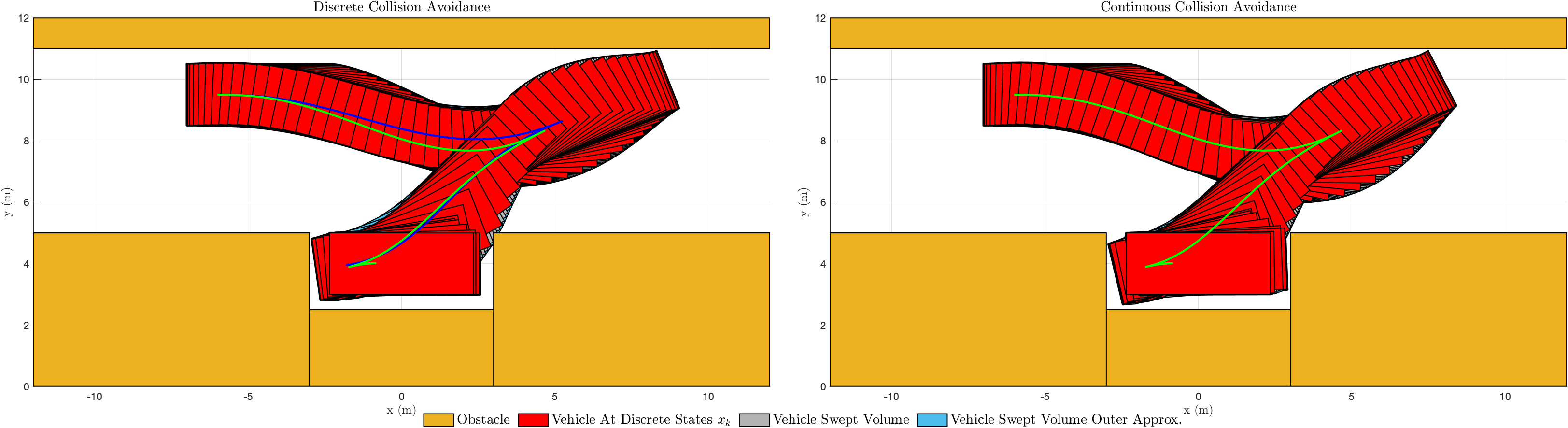
In [3], the authors consider parallel parking of a rectangular vehicle using discrete collision avoidance conditions. Carefully examining the resulting figure (or running the code [3]) it is clear that the vehicle’s front right corner passes through part of the obstacle between discrete time indices. We replicated this example using our method for both discrete and continuous collision avoidance. As expected, the discrete collision avoidance result clips the corner (the swept volume passes over the corner). By planning with continuous collision avoidance we prevent this behavior.

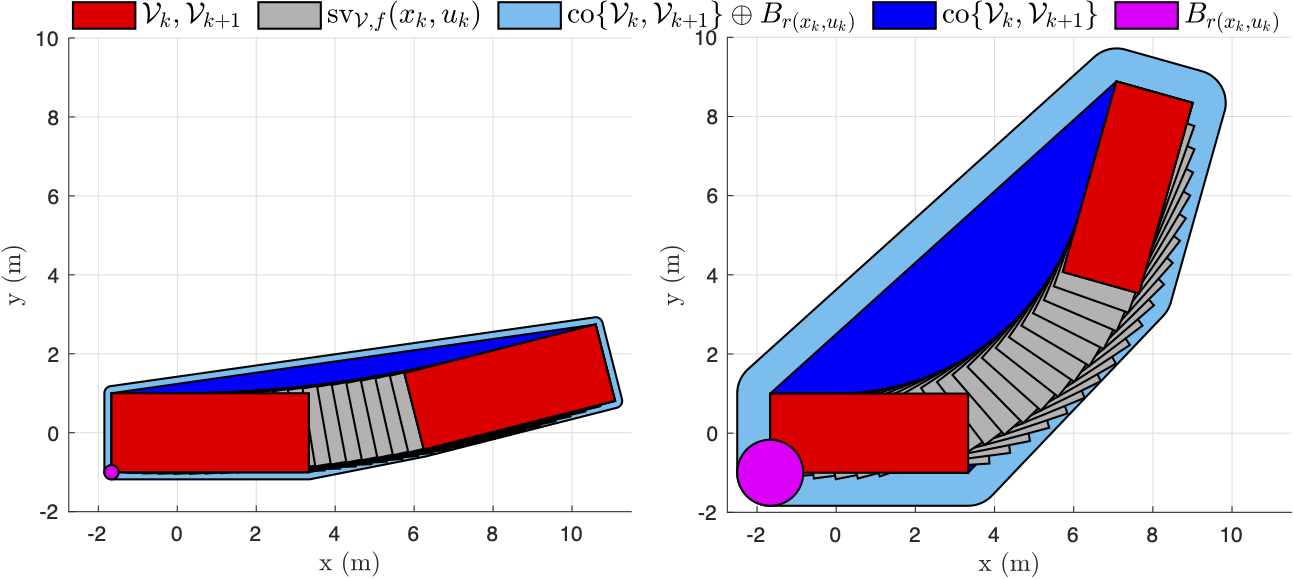
We achieve continuous collision avoidance by developing a novel outer approximation of the swept volume. This approximation consists of finding a Euclidean ball which accounts for the extent to which the convex hull of start and end poses underestimates the true swept volume. We make the Euclidean ball radius be a function of the system state and input. Thus when we are traveling straight (and the convex hull is exact) we introduce no additional inflation to capture the swept volume. When turning, the convex hull is neither an inner nor outer approximation of the convex hull. The Euclidean ball inflates our hull to fully capture the swept volume. Although this introduces conservatism, with practical time steps the resulting conservatism is negligible as shown in the figure above.

To our knowledge this is the first method for rigorously enforcing continuos collision avoidance within optimization-based motion planning algorithms. Further, our method supports a more general class of convex geometries beyond that of [1]-[3]. Lastly, for the case of compact polytopes and ellipsoids our method introduces fewer additional variables than [1]-[3], leading to smaller nonlinear programs. Below we show a Dubin’s car with rectangular geometry navigating around various obstacles.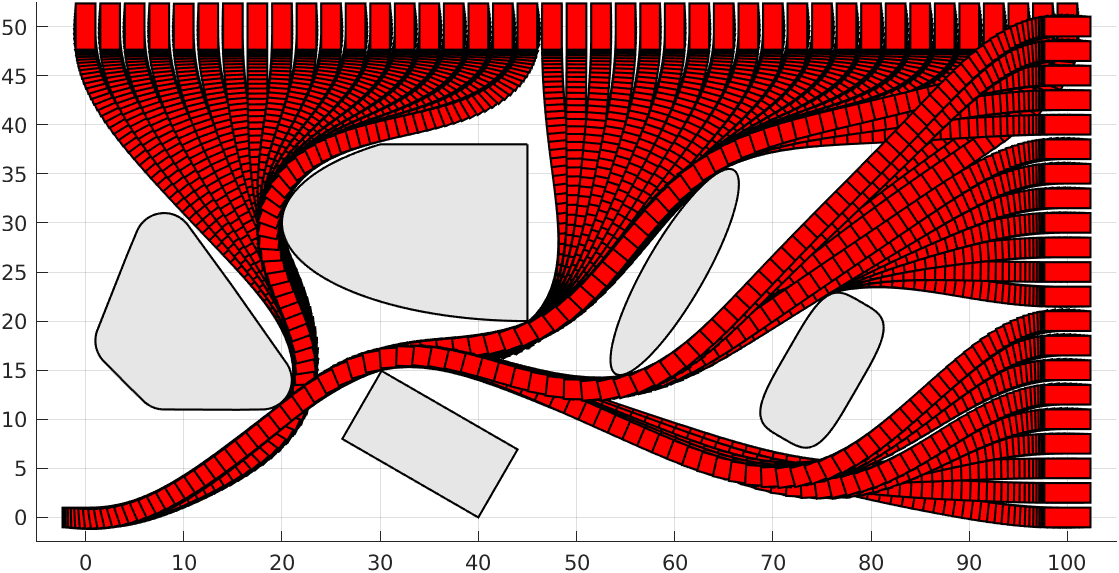

We are currently extending this framework to address trajectory optimization in the presence of uncertainty.

[1] R. B. Patel and P. J. Goulart, “Trajectory generation for aircraft avoidance maneuvers using online optimization,” Journal of Guidance, Control, and Dynamics, vol. 34, no. 1, pp. 218–230, 2011.

[2] M. Gerdts, R. Henrion, D. H ̈omberg, and C. Landry, “Path planning and collision avoidance for robots,” Numerical Algebra, Control and Optimization, vol. 2, no. 3, pp. 437–463, 2012.

[3] X. Zhang, A. Liniger, and F. Borrelli, “Optimization-based colli- sion avoidance,” IEEE Transactions on Control Systems Technology, vol. 29, no. 3, pp. 972–983, 2021. https://github.com/XiaojingGeorgeZhang/OBCA